Grado:Tercero
Área: Matemáticas
Herramientas del estudiante: Implemento didactico, revistas, información de Internet, libros de apoyo.
Tiempo: 2 horas
Pregunta: ¿como hallar la mitad de una cantidad numérica?
Logros del estudiante: Motivar al estudiante sobre el aprendizaje y clasificación del mundo de la matemática, se hará mediante juegos, talleres, demostraciones didácticas para que el estudiante tenga interés acerca del tema.
Palabras claves:
Adición: Es una operación básica de la aritmética de los números naturales, enteros, racionales, reales y complejos; por su naturalidad, que se representa con el signo
Signo: La palabra signo deriva del vocablo latino signum. Se trata de un término que describe a un elemento, fenómeno o acción material que, por convención o naturaleza.
Logaritmo: Número real positivo, en una base de logaritmo determinada, es el exponente al cual hay que elevar la base para obtener dicho número.
Numero: En ciencia, es una abstracción que representa una cantidad o una magnitud. En matemáticas un número puede representar una cantidad métrica o más generalmente un elemento de un sistema numérico.
Operación: Conjunto de reglas que permiten obtener otras cantidades o expresiones, suma resta.
.

Cuando hablamos de operaciones nos referimos a ejecuciones o maniobras metódicas y sistemáticas sobre cuerpos, números, datos, etcétera, para lograr un determinado fin. En Matemática conocemos operaciones de suma, resta, multiplicación y división, ya sea con números enteros o fraccionarios, donde se obtiene un nuevo elemento a partir de dos elementos dados. Existen operaciones aritméticas directas o de composición, como la suma, la multiplicación y la potencialmente, y las operaciones inversas a ellas, que son la resta, la división, la radiación y la logaritmo. Las operaciones financieras consisten en sustituir o intercambiar ciertos capitales por otros equivalentes, aplicando una ley financiera, por ejemplo cuando se contrata un préstamo bancario.Nuestra mente también realiza actividades u operaciones llamadas cognitivas como la observación la comparación, la clasificación y análisis de datos, la interpretación, la formulación de hipótesis.

La Investigación de Operaciones o Investigación Operativa es una disciplina donde las primeras actividades formales se dieron en Inglaterra en la Segunda Guerra Mundial, cuando se encarga a un grupo de científicos ingleses el diseño de herramientas cuantitativas para el apoyo a la toma de decisiones acerca de la mejor utilización de materiales bélicos. Se presume que el nombre de Investigación de Operaciones fue dado aparentemente porque el equipo de científicos estaba llevando a cabo la actividad de Investigar Operaciones (militares).Una vez terminada la guerra las ideas utilizadas con fines bélicos fueron adaptadas para mejorar la eficiencia y la productividad del sector civil.Una de las áreas principales de la Investigación de Operaciones es la Optimización o Programación Matemática. La Optimizan se relaciona con problemas de minimizar o maximizar una función (objetivo).
Como operación matemática, la suma o adhesión consiste en añadir dos números o más para obtener una cantidad total. El proceso también permite reunir dos grupos de cosas para obtener un único conjunto. Por ejemplo: si tengo tres manzanas y tomo otras dos, tendré cinco manzanas (3+2=5). Lo mencionado respecto a las cantidades homogéneas hace referencia a que, si a cinco manzanas le sumo cuatro peras, obtendré como resultado nueve, pero no nueve manzanas o nueve peras. La operación lógica es la misma (5+4=9), pero las cantidades no son homogéneas, a menos que se agrupen las manzanas y las peras en el conjunto de las frutas.Es importante señalar que la suma y la resta son las operaciones matemáticas más básicas y las primeras que se aprenden durante la infancia; la forma más sencilla de contar consiste en la acción repetitiva de sumar uno (1+1+1+1=4).. Las cuáles a su vez cuentan con su par complejo, en el caso de la suma su par es la multiplicación y en el de la resta, la división


Existen tres tipos de propiedades: propiedad conmutativa, propiedad asociativa,propiedad distributiva.
Es una propiedad fundamental que tienen algunas operaciones según la cual el resultado de operar dos elementos no depende del orden en que se toman. Esto se cumple en la adición y la multiplicación ordinarias: el orden de los sumando no altera la suma, o el orden de los factores no altera el producto.
La conmutativo de las operaciones elementales de sumar y multiplicar ya era conocida implícitamente desde la antigüedad, aunque no fue llamada así hasta principios del siglo XIX, época en que las matemáticas contemporáneas empezaban.

Es decir, en una expresión asociativa con dos o más ocurrencias seguidas de un mismo operador asociativo, el orden en que se ejecuten las operaciones no altera el resultado, siempre y cuando se mantenga intacta la secuencia de los operando. En otras palabras, reorganizar los paren-tisis en una expresión asociativa no cambia su valor final. La suma y el producto de números reales cumplen la propiedad asociativa, siendo válidas las igualdades a + (b + c) = (a + b) para la suma y a * (b * c) = (a * b) * c para la multiplicación. En ambas, la ubicación de los paréntesis no altera el resultado. No tese que los operando han se han mantenido en su posición original dentro de la expresión. Muchas operaciones importantes son no asociativas, por ejemplo la resta y la exponencial. Las expresiones que contienen tanto operaciones asociativas como operaciones no asociativas dan como resultado expresiones no asociativas.

En matemáticas y en particular en álgebra abstracta, la distributiva es la propiedad de los operaciones binarias que generaliza la propiedad distributiva del álgebra elemental La propiedad distributiva de la multiplicación sobre la suma en álgebra elemental es aquella en la que el resultado de un número multiplicado por la suma de dos o más sumando, es igual a la suma de los productos de cada sumando por ese número.

El concepto de resta designa a una de las operaciones matemáticas por excelencia, junto a la división, suma y multiplicación. Sin lugar a dudas es una de las operaciones que más usamos en nuestra vida cotidiana, en aquellas situaciones que implican la realización de cuentas, especialmente cuando se trata de dinero que debe egresar de nuestro bolsillo o cuentas por alguna causa. Básicamente, la operación de la resta consiste en encontrar la diferencia que existe entre dos cantidades. Cabe destacarse que la operación de la resta se simboliza con el signo menos (-). Formalmente a la primera cantidad se la denomina minuendo, .Vale indicarse que a la resta se la suele denominar como sustracción. En el uso coloquial la palabra resta se usa extendidamente cuando se quiere indicar que una persona, su presencia digamos, no suma en algún lugar o en alguna situación por la forma que tiene de ser o de comportarse que es desagradable. La presencia de tu hermano, con ese modo tan rudo, sin dudas resta siempre en nuestros encuentros.

El minuendo, en una resta, es el primero de los dos números que intervienen y es la cantidad de la que debe restarse otra. Cantidad a la que se le resta otra cantidad para obtener la diferencia: en la resta 5 - 3 = 2, elminuendo es 5 y el sustraendo es 3.
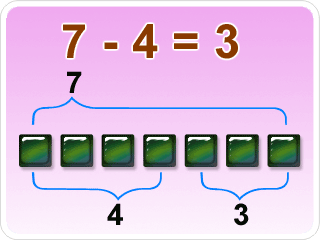
En la operación matemática de restar, cantidad que se resta: en la resta 10 - 8, el sustraendo es 8. Cantidad que ha de restarse de otra.

La multiplicación consiste en encontrar un resultado x a partir de la repetición de un número por x cantidad de veces y tal como nos lo indica otro número, por ejemplo, 6 x 4, esto implica repetir cuatro veces el número seis lo que nos da como resultado 24; al 6 y al 4 se los denomina formalmente factores y al resultado, 24, producto. El fin de la operación de multiplicación es la de hallar el producto a partir de los factores propuestos. Cabe destacar, que la multiplicación es exactamente lo mismo que sumar tantas veces como indique un número un valor dado, entonces, en el caso que propusimos 6+6+6+6 = 24.
Asociada a esta operación y para hacer mucho más sencilla la tarea, se han creado las tablas de multiplicación, existen nueve tablas: la del 1, la del 2, la del 3, la del 4, la del 5, la del 6, la del 7, la del 8, la del 9 y la del 10. Tales tablas son enseñadas durante los primeros años de escuela en la asignatura de matemáticas.
La multiplicación de un número por una suma es igual a la suma de las multiplicaciones de dicho número por cada uno de los sumando.
Pongamos un ejemplo: 2 x (3 + 5) Según la propiedad distributiva 2 x (3 + 5) será igual a 2 x 3 + 2 x 5, Comprobemos si esto es cierto.
2 x (3 + 5) = 2 x 8 = 16
2 x 3 + 2 x 5 = 6 + 10 = 16
Ambas nos dan como resultado 16, por lo que queda demostrada la propiedad distributiva de la multiplicación.
El orden de los factores no varía el producto. Vamos a ver un ejemplo de la propiedad conmutativa. El resultado de multiplicar 10 x 3 será igual que al multiplicar 3 x 10. Aunque cambiemos el orden de los factores el resultado seguirá siendo 30.

El modo de agrupar los factores no varía el resultado de la multiplicación. Pongamos un ejemplo de la propiedad asociativa de la multiplicación. En este caso, como mostramos en la imagen, nos dará el mismo resultado si multiplicamos 3 x 2 y después lo multiplicamos por 5, que si multiplicamos 2 x 5 y después lo multiplicamos por 3.
- La división matemática, por lo tanto, busca el valor denominado cociente, que representa la cantidad de veces que aparece un número (llamado dividendo) en otro (conocido como divisor), a través de un procedimiento estandarizado, el cual puede variar de acuerdo al país, aunque no significativamente.
- La división puede resultar exacta (si el resto es cero) o inexacta (cuando el resto es diferente a cero). Cuando la división es inexacta, quiere decir que el divisor no aparece contenido una cantidad de veces exacta en el dividendo, sino que queda un resto. Por ejemplo: 6 / 2 = 3 (“seis dividido dos es igual a tres”) es una división exacta.La operación inversa a la división es la multiplicación. Siguiendo con el ejemplo anterior, puede decirse que 3 x 2 = 6 (“tres multiplicado por dos es igual a seis”) ya que el dividendo es igual al cociente multiplicado por el divisor más el resto (6 = 3 x 2 + 0).


No podemos dividir por cero: ya que no existe ningún cociente que multiplicado por 0 sea igual al dividendo.
Propiedad de la división exacta: llamamos división exacta a la división en la que el dividendo es igual al divisor por el cociente y el resto es cero. Por ejemplo: 10 ÷ 2 = 2 x 5
Propiedad de la división inexacta o entera: llamamos división inexacta o entera a la división en la que el dividendo es igual al divisor por el cociente más el resto. Es decir: D= d x c + r. Por ejemplo: 30 ÷ 7 = 4 (resto 2); por lo tanto, divisor x cociente + resto = 7 x 4 + 2 = 28 + 2 = 30 (dividendo).
Lápiz, borrador, tijeras, material didáctico (revistas, información de Internet ) libros de apoyo, crucigramas.
- Empezaremos con la presentación de docentes, mediante un saludo
-Haremos un llamado de lista, para conocernos mas entre nosotros y podamos estar mas a gusto.(se hará mediante el juego del bolígrafo loco )
- Procederemos a realizar una oración para estar en paz y en contacto con Dios para tener una excelente energía durante la explicación.
Empezaremos con la proyección de un vídeo en un vídeo bin, donde se les explicara las cuatro operaciones básicas (suma, resta, multiplicación, división), luego de la proyección del vídeo, explicaremos cada operación por medio de juegos didácticos donde los niños van a sentir entusiasmo por la clase, después de tener claro los conceptos realizaremos una mesa redonda donde los niños podrán participar activamente ya sea con preguntas o con aportes, finalmente realizaremos las siguientes actividades.
click para reforzar tus conocimientos, no lo pienses tanto!
Luego de realizar las actividades del link anterior, finalizaremos la clase por medio de un juego mas exactamente el juego de la semilla ( Con música relajante de fondo y luz tenue, simbolizaremos el crecimiento de un árbol.Comenzaremos por ponernos de rodillas en el suelo con la cabeza agachada y los brazos extendidos hacia adelante, como si fuésemos gatitos ) y así los niños relajaran la mente, luego de este animado juego realizaremos nuestra despedida y agradecimiento por la atención prestada en la clase
COMPETENCIA DE RAZONAMIENTO: El estudiante desarrollara esta competencia ya que podrá resolver problemas matemáticos, ademas la lógica del estudiante se
desarrollara con mayor fortaleza y con esto el estudiante teniendo material físico tendrá la posibilidad de desarrollar actividades, talleres por si
solo.
COMPETENCIA COGNITIVA:El estudiante desarrollara esta competencia a partir de las actividades individuales o grupales, participando y desarrollando aquellas actividades de razonamiento matemático como lo es la suma, la resta, la multiplicación, la división.. con esto el niño fortalecerá esta competencia poco a poco.
COMPETENCIA COMUNICATIVA: El estudiante desarrollara esta competencia a partir de la socializacion de los trabajos escritos u orales ademas en actividades grupales. con esto el estudiante tendrá mas facilidad al hablar y comunicarse con sus compañeros.
-Reconocimiento de las propiedades matematicas conmutativas o asociativas
-Por medio de actividades ludicas generando facilidad en el aprendizaje y comprencion para asi aplicar evaluacion escrita retomando los temas vistos



























No hay comentarios:
Publicar un comentario